Recent work introduced the vast unfolding of community detection in large networks, in which a heuristic methodology not only identifies communities, but also measures the density between nodes in modules that highlight the strength of a subcommunity. It was shown that such clustering methodologies can facilitate community detection with the benefits that include exceeding other clustering algorithms in time complexity. In this paper, we focus on using CESNA (Communities from Edge Structure and Node Attributes) in order to combine both methodologies to see if we can categorize music artists by genres based on the Spotify playlists they are in. By using a combination of the generated network’s edges and the attributes of each artist, CESNA was able to construct 7 distinct communities with 53% of artists in each community matching the top genres (such as indie-pop) in each respective community and 82% of artists matching the general genre of each community.
Introduction
Technological innovations during the past few decades, including the rise of computers, the internet, and social media, have accelerated the size and strength of data networks. When analyzing the data behind various data networks, communities form naturally within them through connections between individual points of data, or nodes. These communities are typically defined by a common variable such as physical location, political alignment, or interest in a public figure. However, as more individual nodes of data are added to the data collection, the number of connections between nodes and the number of communities formed to represent these connections grows exponentially, creating difficult problems to overcome when analyzing the data in a timely manner.
Traditional approaches for community detection, such as the planted clique problem, have focused on identifying dense subgraphs in the network. However, these methods may not be optimal for networks with overlapping communities or complex features. This has led to the development of alternative approaches, such as CESNA, that leverage additional information beyond the network topology. By considering both edges and features, CESNA can provide a more nuanced understanding of the communities in the network, which is essential for many real-world applications.
CESNA takes a different approach for detecting communities by using a combination of the network architecture as well as the specific features of each node. By considering both sources of information from the data independently, CESNA is able to better understand and assess which nodes best belong in each community. While there do exist other algorithms which take both edges and features into account, CESNA is able to outperform them when dealing with networks that feature overlapping communities, an important distinction given how interconnected some communities can be in networks.
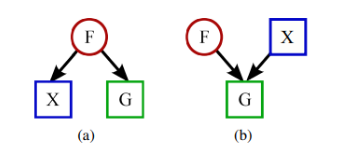
Two ways of modeling the statistical relationship between a graph G, attributes X, and Communities F. Circles represent variables that need to be inferred while squares represent observed variables.
Data
Our primary source of data is a dataset of Spotify playlists collected by Andrew Maranh˜ao, which is freely available on Kaggle. This dataset was collected using a subset of users who published their nowplaying tweets via Spotify. This tabular dataset lists a row for each song that was tweeted out, containing the name of the song, the artist of the song, and the playlist that song was playing from. While the data also contained the user IDs of each person who tweeted the track they were listening to, our model does not take personal information as input.
We began our initial analysis of the dataset by removing any rows that contained missing information as well as playlists that only contained a single artist. We then randomly sampled 2000 playlists from our dataset, and increased the threshold to only keeping artists that were in at least 10 playlists. A graph was then generated by iterating through artists within playlists and generating edge weights between artist nodes. Initially, this gives us a novel perspective on how artists are connected through their appearances in playlists.
Visual insight into how artists are connected through their appearances in playlists.
Methods
On a technical level, in network G, each node has K attributes, and there are C communities in total. The node attributes are represented in a binary matrix as X where Xu,k is the k-th attribute of node u. Additionally, we consider a community membership matrix F, where we assume that each node u has a non-negative affiliation weight Fu,c ∈ [0, ∞) to community c. If Fu,c = 0 then node u does not belong to community c.
For implementation, the adjacency matrix is constructed from nodes defined to be artists, where an edge is denoted by two artists existing in the same playlist. Our node attribute is constructed by calculating total playlist appearances by artist and identifying the top 25% threshold of appearance count. The attribute is the binary representation of whether that artist’s total appearances is above the threshold.
The CESNA algorithm infers communities through four assumptions:
Nodes that belong to the same communities are likely to be connected to each other Nodes can belong to multiple communities Nodes with more communities in common are more likely to be connected than those with less in common Nodes in the same community share common attributes These assumptions are satisfied because:
Edges are created from shared community memberships (edges are created if artists are in the same playlist). Each node represented in the community membership matrix F is considered an independent variable which allows a node to belong to multiple communities. Each member in community c has independent connections, so those with more communities in common are more likely to be connected than those with less. We can predict the value of each node’s attributes based on a node’s community membership. The objective function we are trying to solve is then F̂, Ŵ = argmax ℒ(G) + ℒ(X) where ℒ(G) = log P(G|F) and ℒ(X) = log P(X|F, W). We break ℒ(G) and ℒ(X) into two subproblems by fixing community memberships F and weights W for each node and update F and W at the end of each iteration of gradient ascent.
Results
Using the CESNA algorithm, we identified seven distinct communities from the Spotify dataset. To assess the accuracy of our algorithm, we evaluated the top three genres in each community and computed the percentage of nodes within each community that have any of these three genres. We also used generalized genre for our accuracy metric here because there are several sub-genres of a main genre for example indie-pop and dance-pop which we believe that including all under the term pop is appropriate.
The same network, now assigning a color to each artist based on which community CESNA found them most likely to be in.
The first community detected belongs to the rock genre, containing 496 edges or playlists and includes popular bands such as Bon Iver and One Direction. The genre accuracy of this community is approximately 45.4%, while the accuracy of the generalized genre improved to 78.8%.
The second community we identified is a dance pop genre group with only five edges, including artists such as Charli XCX, Demi Lovato, will.i.am, Naughty Boy, and The Pussycat Dolls. Given the small size of this community, both the genre accuracy and the generalized genre accuracy are 100%.
The third community is also a dance pop genre group with 76 edges, including artists such as John Mayer and Adele. The genre accuracy of this community is 60.5%, and the accuracy of the generalized genre is about 87%.
The fourth community is a hip hop genre group with only eight edges, featuring popular artists like Kendrick Lamar, Drake, and Lil Wayne. The genres of this community include hip-hop, rap, and pop. The genre accuracy of this community is 75%, and the accuracy of the generalized genre improves to 87.5%.
The fifth community is another dance pop genre group with 26 edges, including artists such as Britney Spears and Snoop Dogg. The genres of this community include dance pop, pop, and pop rap. The genre accuracy is 69.2%, and the generalized genre accuracy is 88.5%.
The sixth community is the second community in the rock genre group with a generalized genre of rock which has 17 edges including artists such as Beck and Red Hot Chili Peppers. The genres of this community include rock, modern rock, and pop rock. The genre accuracy of this community is about 65%, and it improves to 94% when we generalize the genre.
Finally, the last community we detected in our model also belongs to the rock genre with a generalized genre of rock. It has a community size of 148 edges including artists such as Coldplay and Arctic Monkeys. The genres of this community include rock, pop, and dance. The genre accuracy of this community is about 68%, and the generalized genre accuracy is 86%.
Overall, the total accuracy of the original genres associated with each artist is 53%, which improves to 82% when we generalize the genres. Looking at a single data point in it’s original form, we are only able to identify the playlists an artist is featured on. Using this network we can quickly identify several similar artists, not just limited to those in the same playlists. In a practical sense, a network like this can be used to generate new playlists or discover similar artists.